Kwadrat Lolcia: Punkty A=(1,3), C=(7,1) są przeciwległymi wieszchołkami kwadratu ABCD. Wyznacz współrzędne pozostałych wieszchołkówbtego kwadratu. Proszę o pomoc

AROB: pomogę

Lolcia: Bardz proszę

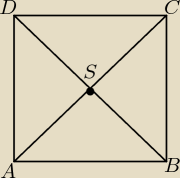
AROB: Dane: A(1,3), C(7,1), B,D = ? − Wyznaczamy punkt S − środek odcinka AC.

	xA + xC		1+7
xS =		=		= 4
	2		2

	yA+yC		1+3
yS =		=		= 2, czyli S(4,2)
	2		2

− Wyznaczamy współczynnik kierunkowy prostej AC:

	yC−yA		1−3		1
aAC =		=		= −
	xC−xA		7−1		3

− Wyznaczamy współczynnik kier. prostej BD ⊥ AC :

	1
aBD = −		= 3
	aAC

− Wyznaczamy równanie prostej BD przechodzącej przez punkty B i S: y − y_S = a_BD (x − x_S) y − 2 = 3(x − 4) y = 3x − 12 + 2 ⇒ y = 3x − 10 − Punkt B ∊ BD, czyli y_B = 3x_B − 10 − Obliczamy długość przekątnej AC: IACI = √(x_C−x_A)² + (y_C−y_A)² = √(7−1)² + (1−3)² = = √40 = 2√10 Stąd : ISBI = √10. − Do wzoru na długość odcinka SB podstawiamy y_B = 3x_B − 10 : ISBI = √(x_B−x_S)²+(y_ByS)² √10 = √(x_B − 4)² + (3x_B−10−2)² /² 10 = (x_B)² + (3x_B − 12)² 10 =x_B² −8x_B +16 + 9x_B² − 72x_B + 144 10x_B² − 80x_B + 150 = 0 x_B² − 8x_B + 15 = 0 Δ = 4, √Δ = 2, x_B = 5 lub x_B = 3 Zatem: dla x_B = 5, y_B = 3*5−10 = 5 (to będzie D) dla x_B= 3, y_B = 3*3−10=−1 Odp. Szukane punkty to: D(5,5), B(3, −1).

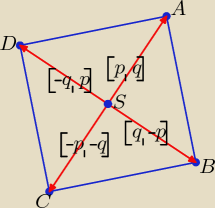
Bogdan: Można to zadanie z kwadratem rozwiązać wektorami wg schematu pokazanego na rysunku. A(1, 3), C(7, 1), S(4, 2) Wektory (nie wprowadzam znaku strzałki nad nazwą wektora): SA = [3, −1], SB = [−1, −3] ⇒ B(4 + 1, 2 + 3) = (5, 5), SC = [−3, 1] ⇒ C(4 + 3, 2 − 1] = (7, 1), SD = [1, 3] ⇒ D(4 − 1, 2 − 3) = (3, −1)

Sleeper: Bogdan a możesz powiedzieć z czego wynika ten rysunek i zmiana znaków? p i q metoda wydaje sie super ale jej nie rozumiem.

Aga1.: A może ja spróbuję Ci wyjaśnić. Wektory SA i SC są przeciwne[p,q] i [−p,−q] w drugim zmieniasz znaki na przeciwne.( np[−3,4] i [3,−4] Wektory SA i SD są prostopadłe [p,q] i [q, −p] W drugim zmieniasz kolejność i znak jednej współrzędnej, np. [3,4] i [4,−3]